Valódi és virtuális téridom:
A WEB-KÚP
avagy egy virtuális téridő-energetikai geometria vázlata
Ha a világháló térgeometriájáról beszélünk, el kell szakadnunk azoktól a vízióktól, melyeket az eddig ismert geometriák tápláltak képzeletünkbe – ide értve a nem-euklideszi geometriákat is –, és pusztán az idomok definícióira kell szorítkoznunk. Ezt minden további nélkül megtehetjük, hiszen semmi akadálya sincs annak, hogy akármilyen virtuális dimenziót, illetve az abban fellelhető/létrejövő entitásokat kvázi-geometriai térként/objektumokként értelmezzük.
Ennek megfelelően: Pontként határozhatjuk meg a hálónak azokat a helyeit, melyek egy email- vagy honlap-cím beírásával, illetve hiperhivatkozás/link beírásával és rákattintással megközelíthetők. Nem minősülnek WEB-geometriai pontnak a világhálón található inaktív objektumok (szövegek, képek, mozgóképek, stb.), mert ezek a dolgok WEB-geometriai szempontból dimenzió előttiek. (Ugyanígy nem alkotja a térgeometria tárgyát az a valami, melynek 1-nél kevesebb dimenzióban van kiterjedése. A térgeometria 1-dimenziós objektuma a pont.)
A ponttól pontig történő ugrás két pontot foglal magában, ez tehát vonal; hogy egyenes-e vagy görbe, az a WEB viszonyai között értelmezhetetlen kérdés. A vonal természetesen tetszőleges számú pontot foglalhat magában, és mindaddig egyenesként értelmezhetjük, amíg a kiindulásához vissza nem vezet. Ad absurdum
az a legkisebb webgeometriai kör, ha két honlapon két link kölcsönösen egymás oldalára mutat.
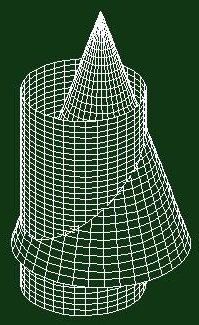
Miután a kúpot úgy határozhatjuk meg, mint egy kört, melynek ívét alkotó valamennyi pontjából szakaszt bocsátottunk egy adott pontba – nevezetesen a kúp csúcsát jelző pontba –, a virtuális WEB-kúpot is könnyen meghatározhatjuk: alaplapját egy WEB-kör alkotja az imént leírtaknak megfelelően, csúcsa pedig egy olyan email-cím, laphely vagy hiperhivatkozás/link, ahonnan a kör minden pontja elérhető, közvetlenül, közbenső pont beiktatása nélkül; míg a kör pontjai egymás felől nem közelíthetők meg (a szomszédos pontokat kivéve természetesen). Vagyis
a WEB-kúp alapkörének szomszédos pontjai egymásból közvetlenül elérhetők, míg a nem szomszédos pontok mind egyetlen közbenső pont, a kúp csúcspontja közbeiktatásával érhetők el.
Azok a pontok, melyek a kör pontjaiból a csúcs beiktatása nélkül elérhetők, de nem alkotnak a kör valamely pontjával szomszédos pontpárt, nem részei a WEB-kúpnak. Természetesen minden pont tetszés szerinti WEB-test alkotó-pontja lehet. Ugyanakkor: ha van olyan pont, mely két szomszédponttal rendelkezik a körön belül, tehát feltehetjük, hogy része a WEB-körnek, ugyanakkor nincs kapcsolata a kúp csúcspontjával, úgynevezett fattyúpont. A kúpnak valójában ez sem eleme.
A WEB-kúp valódi virtuális téridom, mert létezéséhez folytonos virtuális energia-bevitel szükséges.
Ezzel szemben: ha létrehozunk egy zárt hálózatot, kialakítunk benne egy virtuális téridomot, majd a rendszert lezárjuk, a rendszer fagyott rendszerré változik, amelyben csak látszólagos virtuális objektumok találhatók.
A valódi virtuális térben, egy valódi virtuális idom (pl. WEB-kúp) pontjai szüntelen fluktuációban vannak, amennyiben szüntelenül kiesnek olyan pontok, melyek a használat során elvesztik korábbi sajátosságaikat (pl. hogy csak két pontszomszédjuk van, illetve hogy a kúp többi pontjával egyetlen közbenső pont, a kúp csúcspontja közvetítésével kapcsolódnak össze), ugyanakkor szüntelenül újabb pontok keletkeznek, melyek megfelelnek az imént ismertetett definícióknak.
Ebből következik, hogy a WEB-geometria alakzatait magukat nem, csupán pillanatnyi állapotukat ábrázolhatjuk. A szakadatlan állapotváltozás azonban azzal jár, hogy
az ábrázolt WEB-geometriai alakzat mindig múltbeli.
Jelene, azaz (Husserl fenomenológiai időelméletének megfelelő) retenció-periódusa az idom pontjaiban észlelhető két egérkattintás közti intervallum. A retenció-perióduson belül a WEB-geometriai idom tagolhatatlan és oszthatatlan, azaz fagyott rendszernek tekinthető. Ugyanígy a fagyott rendszer is valódi virtuális rendszerré válik, ha a rendszerbe belép valaki. Ez a WEB-alakzatok egzisztenciális paradoxona.
Bodor Béla
A fenti vázlat az UngParty 2003-as identifikciós projektumának egyik sarkalatos szövegténye.
Lásd még: Linkhálózat építése a szemantikus weben. Linképítés – szemantikus weboldal optimalizálás. Identifikció: képzetes szevak lexikonja